1. 힙과 우선순위 큐 개념
힙은 heap property를 만족하는 완전 이진 트리를 말한다. heap property에 따라 두 가지 종류로 힙을 분류한다. heap property는 힙에서 부모 노드와 자식 노드 사이에 존재하는 조건인데, 부모 노드가 자식 노드보다 커야 한다는 heap property를 만족하는 힙은 최대 힙, 반대로 부모 노드가 자식 노드보다 작아야 한다는 heap property를 만족하는 힙은 최소 힙이라고 한다. 트리는 재귀적인 구조이기 때문에 최대 힙의 루트 노드에 가장 큰 값이 오고, 최소 힙의 루트 노드엔 가장 작은 값이 오게 된다. 트리를 구현할 때 연결 리스트 혹은 배열로 구현할 수 있는데 완전 이진 트리는 보통 배열에 저장한다. 배열의 인덱스와 노드 번호를 매핑시키면 노드를 배열에 연속적으로 저장할 수 있기 때문이다. 또한 배열은 중간 인덱스에서 삽입, 삭제하는 연산이 비효율적이지만, 힙의 삽입, 삭제는 중간이 아닌 마지막 노드에서 일어나기 때문에 배열에 구현해도 삽입, 삭제가 비효율적이지 않다. 힙의 가장 큰 장점은 최댓값 혹은 최솟값을 찾는 연산의 효율성이다. 힙을 쓰지 않고 최댓값 혹은 최솟값을 구하기 위해선 순차 탐색 혹은 정렬을 해야 하는데 순차 탐색은 시간 복잡도가 , 정렬은 빨라도 이다. 반면 힙에서 어떤 노드를 삽입, 삭제 후 루트 노드에 최댓값 혹은 최솟값이 설정되는 연산의 시간 복잡도는 이다. 이런 시간 복잡도가 나올 수 있는 이유는 힙의 노드를 올바른 곳에 위치시키는 과정은 heap property를 만족할 때까지 부모 노드, 자식 노드를 비교 후 스왑하는 것인데, 이 과정은 트리 높이에 비례하기 때문이다. 완전 이진 트리의 높이를 , 트리 노드 개수를 이라고할 때, 는 의 근사치다. 이것을 생각하면 는 에 거의 비례하기 때문에 트리 높이에 비례하는 연산은 시간 복잡도가 이 된다. 우선순위 큐를 구현할 때 보통 힙으로 구현하는데, 힙의 최댓값, 최솟값을 효율적으로 찾을 수 있는 특성이 우선순위 큐를 구현하기에 딱 맞는 특성이기 때문이다. 우선순위 큐는 값들을 넣었을 때 꺼내는 순서가 우선순위 순서로 나오는 자료구조이다. 최소힙, 최대힙과 마찬가지로 우선순위 큐도 최대 우선순위 큐, 최소 우선순위 큐로 나누기도 한다.
2. 구현 구조
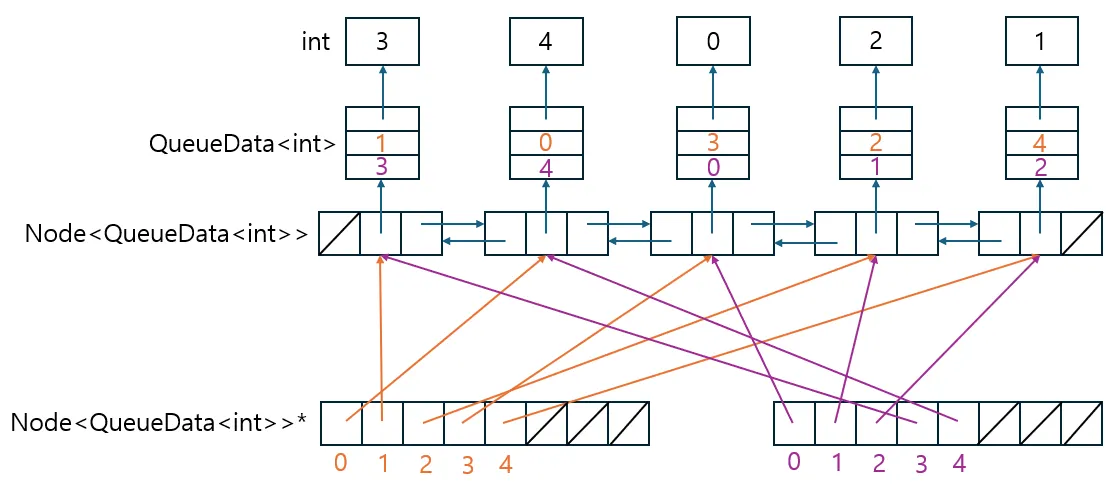
위 그림은 내가 구현한 우선순위 큐 PriorityQueue의 구조다. PriorityQueue는 클래스 템플릿으로 PriorityQueue<int>를 인스턴스화하면 int 데이터를 저장하는 우선순위 큐가 된다. 생성자 중 배열을 받는 생성자가 있는데 배열을 받으면 배열 원소를 복사하여 우선순위 큐에 집어넣는다. 위 그림에선 int배열 { 3, 4, 0, 2, 1 }을 넘긴 경우다. 힙을 구현할 때 보통 배열 하나만 사용한다. 하지만 이 우선순위 큐는 배열을 두 개 사용하는데 최소힙과 최대힙 모두 사용하는 우선순위 큐를 구현했기 때문이다. 이 우선순위 큐는 가장 낮은 우선순위 값과 가장 높은 우선순위 값 모두 시간 복잡도로 꺼낼 수 있다. 왼쪽 아래 배열은 최대힙이고, 오른쪽 아래 배열은 최소힙이다. 배열은 실제 데이터를 갖고 있는 게 아니라 연결 리스트 노드에 대한 포인터다. 포인터를 사용한 이유는 배열에 실제 데이터를 저장해버리면 배열이 두 개이므로 똑같은 데이터가 두 개가 돼 비효율적이기 때문이다. 그리고 두 배열의 데이터를 동기화하는 것이 번거로울 것이다. 노드는 이중 연결 리스트 형태로 연결돼 있는데 삽입, 삭제를 효율적으로 하기 위함이다. 노드는 Node<T> 형태의 구조체 템플릿으로 만든다. T는 노드가 가리키는 데이터의 타입인데 위 그림에선 QueueData<int>가 템플릿 인자로 들어갔다. QueueData<T> 구조체 템플릿은 우선순위를 따지는 데이터에 대한 포인터와 해당 데이터를 소유하고 있는 최대힙, 최소힙 배열 원소의 인덱스 정보를 갖고 있다. 인덱스 정보를 갖고 있는 이유는 삽입, 삭제 연산 시 필요하기 때문이다. 삽입의 경우 힙 배열이 가득 찼을 때 삽입하려는 값이 힙의 가장 낮은 우선순위의 값보다 우선순위가 높은 경우 우선순위가 가장 낮은 값을 삽입 값으로 교체하도록 구현했다. 이 교체를 할 때 최소힙의 루트 노드 값을 변경 후 해당 노드에 해당하는 최대힙 노드의 위치가 변경돼야 하므로 교체되는 최소힙 노드가 최대힙 배열에선 어디 인덱스에 존재하는지 알아야 한다. 삭제의 경우도 비슷한데, 예를 들어 가장 우선순위가 높은 값을 꺼낸다고 할 때 최대힙에서 삭제되는 노드가 최소힙에선 몇 번 인덱스에 해당하는 노드인지 알아야 최소힙을 힙 구조로 다시 재배열할 수 있다.
3. 동작 테스트
#include <iostream>
#include "PriorityQueue.h"
int main()
{
const int arrSize = 7;
int arr[arrSize] = { 3, 2, 1, 6, 5, 7, 4 };
auto fPriorityComparator = [](const int& lower, const int& higher)->bool { return lower < higher; };
// 우선순위 큐 생성
PriorityQueue<int> pq(arr, arrSize, 10, fPriorityComparator);
std::cout << pq << std::endl;
// Max heap: 7 6 4 2 5 1 3
// Min heap: 1 2 3 6 5 7 4
// 삽입
pq.insert(8);
pq.insert(0);
std::cout << pq << std::endl;
// Max heap: 8 7 4 6 5 1 3 2 0
// Min heap: 0 1 3 2 5 7 4 8 6
// 9 삽입 후 힙 배열은 가득 찬다
pq.insert(9);
pq.insert(10);
pq.insert(11);
// -1은 가장 낮은 우선순위 값보다 우선순위가 낮으므로 값 교체가 일어나지 않는다
pq.insert(-1);
std::cout << pq << std::endl;
// Max heap: 11 9 10 8 7 4 3 2 6 5
// Min heap: 2 5 3 6 9 7 4 8 10 11
// 가장 낮은 우선순위 값을 꺼낸다
for (int count = 0; count < 3; ++count)
{
std::cout << pq.extract(HeapType::MIN) << " ";
}
std::cout << std::endl;
// 2 3 4
// 가장 높은 우선순위 값을 꺼낸다
for (int count = 0; count < 3; ++count)
{
std::cout << pq.extract(HeapType::MAX) << " ";
}
std::cout << std::endl << std::endl;
// 11 10 9
std::cout << pq << std::endl;
// Max heap: 8 7 6 5
// Min heap: 5 6 7 8
return 0;
}
C++
복사
Max heap: 7 6 4 2 5 1 3
Min heap: 1 2 3 6 5 7 4
Max heap: 8 7 4 6 5 1 3 2 0
Min heap: 0 1 3 2 5 7 4 8 6
Max heap: 11 9 10 8 7 4 3 2 6 5
Min heap: 2 5 3 6 9 7 4 8 10 11
2 3 4
11 10 9
Max heap: 8 7 6 5
Min heap: 5 6 7 8
C++
복사